correction cinématique

Vitesse

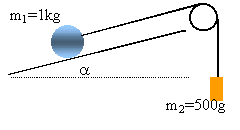
On remonte un seau verticalement à l'aide d'un moteur dont la poulie de diamètre 30 cm tourne à raison de 48 tr/min. Le point A se trouve à l'endroit où la corde tient au seau. B se trouve à la première zone de contact entre la poulie et la corde.
Calculer la vitesse angulaire de la poulie.
A quelle condition le seau est-il animé d'un mouvement rectiligne et uniforme?
Calculer alors le vecteur vitesse de A en justifiant votre réponse.

---

corrigé

---

vitesse angulaire (rad/s) de la poulie : 48 tr/min soit 48/60 = 0,8 tr/s
un tour correspond à 2 p radian s ; 0,8 tour /s correspond à 0,8*2 p = 0,8*2*3,14 = 5,024 rad/s.
Le seau est-il animé d'un mouvement rectiligne et uniforme si la somme vectorielle des forces qui agissent sur lui est nulle ( principe d'inertie). Le seau est soumis à deux forces ( son poids et la tension de la corde) ; ces deux forces se compensent.
vecteur vitesse de A :
La corde s'enroule sur la poulie sans glisser, à chaque tour de poulie il s'enroule une longueur L = 2pR avec R le rayon de la poulie.
La vitesse de la corde est bien égale à la vitesse ciconférentielle de la poulie
vitesse de A(m/s) = vitesse angulaire (rad/s)* rayon (m) de la poulie
v_A=wR =5,024*0,15 = 0,75 m/s.

---

A vélo, Francis constate qu'il effectue 20 tours de pédalier par minute. Le nombre de dents du pédalier étant 3 fois celui du pignon de la roue, exprimer la fréquence de rotation de la roue en tr/min et en tr/s.
- Les roues de son vélo ayant un diamètre de 700 mm, calculer la distance qu'il parcourt en 20 min ?

---

corrigé

---

Le nombre de dents du pédalier étant trois fois plus grand que celui du pignon de la roue, la roue fait 3 tours quand le pédalier fait un tour. Donc 20 tours de pédalier en une minute c'est trois fois plus pour la roue, soit 60 tours / min. La fréquence est le nombre de tours par seconde soit 1 tour /s ou 1 Hz.
distance parcourue en 20 min :
circonférence de la roue : 3,14*diamètre = 3,14*0,7 = 2,198 m
à chaque tour de roue, le vélo parcourt 2,198 m
en une minute la roue fait 60 tours ; en 20 min la roue fait 60*20 = 1200 tours.
distance parcourue en 20 min : 1200*2,198 = 2637 m.



Un disque de meule est en rotation autour d'un axe. L'un de ces points décrit une trajectoire circulaire de rayon r=5,0 cm. Sa vitesse angulaire est constante et égale à 4,7 rad.s^-1.
>Représenter, à l'échelle 1, la trajectoire de ce point.
Calculer sa fréquence de rotation en tour par minute.
Calculer la vitesse de point mobile en un point de sa trajectoire.
Représenter le vecteur vitesse instantanée en deux points de la trajectoire (échelle: 1 cm pour 0,1 m.s^-1)

---

corrigé

---

La trajectoire de ce point est un cercle de 5 cm de rayon.
Un tour correspond à 2 p radians.
vitesse angulaire ( rad/s) = 2 p * fréquence ( tour/s ou Hz)
fréquence = vitesse angulaire / (2 p)=4,7 / (2*3,14) = 0,748 tour/s soit 0,748*60 = 44,9 tours/min.
vitesse (m/s) d'un point A situé à la circonférence= vitesse angulaire (rad/s)* rayon (m) de la poulie
v_A=wR =4,7*0,05 = 0,235 m/s.
Le vecteur vitesse est portée par la tangente à la trajectoire et a toujours le sens du mouvement.

---

1. Un lapin parcourent 150 mètres en 8 secondes. Quelle est sa vitesse ?
2. Un tgv roulent pendant 20 minutes a la vistesse de 280 km/h. Quelle distance a t-il parcouru ?
3. Quel temps en secondes faut-il a un corbeau qui vole a 40 km/h pour rejoindre un arbre qui se trouve a 300 mètres de lui ?
4. La vitesse moyenne d'un coureur cycliste étant 36km/h exprimé cette vitesse mètre seconde.
5. Un cheval galope a 17m/s ; quelle est sa vitesse en km/h ?

---

corrigé

---

La vitesse du lapin est : distance (m)/ durée (s)=150 / 8 = 18,75 m/s on peut aussi calculer la vitesse en km/h : 1 heure = 3600 secondes
en 3600 secondes, le lapin fait: 18,75 * 3600 = 67500m = 67,5 km
La vitesse du lapin est 67,5 km/h.

---

20 minute = 1/3 heure. Le TGV a parcouru: 280/3 = 93,333 km.

---

exprimer la vitesse en m/s : 40000/3600 =11,111 m/s distance parcourue (m) = vitesse (m/s)* temps (s).
temps = distance / vitesse = 300 / 11,111 = 27 secondes.

---

36 km en 1 heure est identique à 36000 m en 3600 s en 1 seconde, il fait: 36000/3600 = 10 m
v = 10 m/s.

---

Le cheval parcourt 17 m en 1 seconde. En 3600 secondes (=1heure), il parcourt: 17 * 3600 = 61200 m = 61,2 km
v = 61,2 km/h.
On étudie le mouvement d'un satellite S dans le referentiel géocentrique. Il décrit un mouvement circulaire uniforme autour de de l'axe des pôles terrestres, dans le plan de l'équateur, dans le même sens que la rotation de la terre, à l'altitude 228 km. Le rayon de la terre vaut R=6380 km.

1. Le satellite effectue un tour complet en 1 h 29 min. Quelle est la vitesse angulaire w_S en rad/h ?
   - Quelle est sa vitesse linéaire en m/s et en km/h ?
2. Calculer la valeur de la vitesse angulaire w_T de la terre en rad/h.
   - Pendant que le satellite a effectué un tour complet, quel est l'angle de rotation de la terre ?
3. Le satellite repasse à la verticale d'une même ville au bout d'une durée F . Exprimer, en fonction de w_S, w_T et de F, l'angle de rotation de la terre a_S et celui du satellite a_T - Comparer a_S et a_T. Calculer F

---

corrigé

---

Un tour correspond à 2 p radians; 1 h 29 min = 3600+29*60=5340 s vitesse angulaire (rad/s) = 2*3,14 / 5340 =1,176 10^-3 rad/s
soit en multipliant par 3600 : w_S = 4,234 rad/h.
La vitesse linéaire (m/s) est égale à la vitesse angulaire (rad/s) fois le rayon de la trajectoire circulaire (m), c'est à dire rayon terrestre + altitude.
v =1,176 10^-3 * (6380+228) 10³ = 7 771 m/s
multiplier par 3,6 pour passer en km/h : 7771*3,6=2,8 10⁴ km/h.

---

vitesse angulaire w_T de la terre : 1 tour ( 2 p radians ) en 24 heures. w_T = 2*3,14 / (24*3600)=7,26 10^-5 rad/s ou 2*3,14/24=0,261 rad/h.
en 1 h 29 min ( soit 5340 s) la terre tourne de : 7,26 10^-5 * 5340 =0,388 rad.

---

Le satellite repasse à la verticale d'une même ville au bout d'une durée F. Ce dernier a effectué un tour de plus que la terre pendant la durée F. angle décrit par le satelitte ( rad) = vitesse angulaire satelitte ( rad/s) * durée en seconde
a_S = w_S F.
angle décrit par la terre pendant la même durée= angle décrit par le satellite - 2 p ( un tour de moins
a_T = w_T F = a_S - 2 p = w_S F- 2 p
w_T F = w_S F- 2 p ;( w_S - w_T )F= 2 p ; F= 2 p/( w_S - w_T )
F=2*3,14 / (1,176 10^-3-7,26 10^-5 )=6,28 / 1,1 10^-3 = 5710 s = 1h 35 min.

correction Ressort

raideur d'un ressort ; travail d'une force ; puissance


On considère un ressort R de constante de raideur k inconnue. Lorsqu'on suspend à son extremité libre une masse m₁ =25 g, sa longueur est L₁=18,5cm ; lorsqu'on suspend une masse m₂=45 g sa longueur est L₂=20,5cm.
Déterminer la valeur de la raideur k et celle de la longueur à vide L₀ du ressort.
 
L'extrémité inférieure du ressort est soumise à :
l'action de la masse, verticale vers le bas, valeur P=mg ( masse en kg)
à la tension du ressort, verticale vers le haut, valeur T= k x ( k : raideur en N/kg et x : allongement en m)
T= mg = kx

m₁g = k(L₁-L₀) = kL₁-kL₀ (1)
m₂g = k(L₂-L₀) = kL₂-kL₀ (2)
(2)-(1) donne : k(L₂-L₁) = (m₂-m₁)g
L₂-L₁ = 0,02 m ; m₂-m₁ = 0,02 kg
k = 0,02*9,8/0,02 = 9,8 N/m.
L₀ = L₁-m₁g/k = 0,185-0,025*9,8 /9,8 = 0,16 m = 16 cm.

---

Déterminer le travail du poids lors de l'allongement du ressort dans le cas où m₂=45 g :
Le travail d'une force constante ne dépend que des positions finale et initiale.
En descente le travail du poids est moteur et vaut :
W=m₂g ( L₂-L₀)
W= 0,045*9,8 *0,045 =0,02 J.

---

Un solide de m =50 kg est en mouvement dans le repère orthonormé (O, i, k).
Il est animé d'un mouvement rectiligne uniforme et il est soumis aux forces P, f₁, f₂ telle que :

Exprimer la force f₂ en fonction des vecteurs i et k.




Correction : D'après le principe d'inertie, la somme vectorielle des forces est nulle.

Calculer les travaux des forces exercées sur le solide entre A et B :
 
Correction : Travail du poids :

---

Travail de f₁ :
Travail de f₂ :

Remarque : la somme des travaux est nulle.

concors kiné strasbourg 2000

concours          kiné Strasbourg 2000


quelle (s) est (sont)          la (les ) affirmation(s) exacte(s) ?  
                   

---

      



Objet laché d'un train 
Données pour les 3 premiers exercices: m =500g ; V=108 km/h ; F = 4 N; h =2m.

Un train roule à la vitesse constante V sur une voie horizontale rectiligne.
Un voyageur lâche par la fenêtre d'un point situé à la hauteur h au dessus du sol un objet de masse m, assimilable à un point matériel.
Le vecteur vitesse de l'objet par rapport au sol est à l'instant du lâcher :

-De direction horizontale, dans le sens du mouvement du train
-De direction verticale, dans le sens inverse du mouvement du train
-Nul
-De direction verticale de haut en bas.

---

corrigé                   

---

          



au moment du lâcher de l'objet, celui ci a la          même vitesse que le train:                   
même norme : 108 /3,6 = 30 m             /s. même direction             horizontale même sens que le mouvement du             train
affirmation 1 exacte, les          autres sont fausses.                                        

---

Etude de la chute
On veut étudier le mouvement de l'objet lors de sa          chute.
Celui ci a été lâché          à la date t=0 au point D , d'altitude h au dessus du          sol.
On représente l'action de l'air sur l'objet par          une force F constante colinéaire au vecteur vitesse          du train et de sens contraire à celle ci.  
On          étudie le mouvement dans un repère          terrestre.

-Le mouvement de l'objet suivant l'axe Ox est             rectiligne uniforme.
-Le mouvement de l'objet suivant l'axe Oz est             rectiligne uniformément varié.
-La trajectoire de l'objet est rectiligne.La trajectoire de l'objet est parabolique
                   

---

corrigé                   

---

             
l Le mouvement n'est pas rectiligne uniforme suivant l'axe          Ox car la somme vectorielle des forces n'est pas nulle          suivant Ox.
le mouvement est uniformément varié sur          l''axe Ox et sur l'axe Oz.  
vecteur vitesse : v_x= -8t+30 et v_y = -10t.  
vecteur position          : x= -4t²+30t y= -5t²+2
la trajectoire n'est ni une droite, ni un arc de parabole          (équation du type y=ax²+bx+c)  

affirmation 2 exacte, les autres          sont fausses.                    

---

Point          d'impact
L'objet touche la voie ferrée en un point I :
affirmations :

-La distance OI est voisine de 17 m. 

-La distance OI est voisine de 15 m. 

-La position du point de la fenêtre où             l'objet a été lâché est au             même instant à la verticale du point             d'impact I. 

-Le point d'impact I dépend de la             résistance de l'air.

---

corrigé                   

---

l'ordonnée du point d'impact est égale          à zéro d'où la valeut du temps          correspondant :                    -5t²+2=0 t²= 0,4 et t = 0,632 s. remplacer t par 0,632 s dans l'expression de l'abscisse          x: x=-4*0,632²+30*0,632 = 17,36          m. pendant 0,636 s le train parcourt à vitesse          constante : 0,636*30=18,96 m. le point d'impact n'est pas à la verticale de la          fenètre. Dans l'expression de l'abscisse OI, la résistance          de l'air intervient.  
affirmations 1 et 4 exactes, les          autres sont fausses.                    

---

satellite
Un satellite artificiel S₁ de masse          m₁ est assimilable à un point          matériel.
Dans un repère géocentrique,          supposé galiléen, son orbite est          assimilée à un cercle de rayon r et de          même centre O que la terre.
Le satellite n'est soumis          qu'à l'attraction terrestre.
Un véhicule          spatial S₂ de masse m₂ est sur la          même orbite que S₁, ses moteurs          étant éteints.
Les astronautes de          S₂ cherchent à rejoindre S₁ en          restant sur la même orbite de rayon r.
Pour cela ils          allument un moteur auxiliaire faisant passer leur vitesse de          v₀ à la valeur v₂.
affirmations :
-La vitesse du satellite est telle que v² r             =GM_T.
-La vitesse du véhicule spatial est             égale à celle du satellite.
-Alors que le véhicule spatial S₂ se             dirige vers S₁ sur orbite de rayon r, à             la vitesse v₂, le moteur exerce une force             tangentielle F dans le sens du mouvement.
-L'expression de cette force F est                                         

---

corrigé                   

---

            Le satellite n'est soumis qu'à la force de          gravitation centripète (dirigée vers le centre          de la terre)                    On utilise le repère de Frenet : suivant l'axe n, la seconde loi de Newton          s'écrit:

Cette vitesse est indépendante de la masse : deux satellites situés sur la même orbite          ont la même vitesse.
Le véhicule reste sur la même orbite que le          satellite lors de l'approche: la force f exercée par          les moteurs est tangentielle.
L'expression de cette force          n'est pas celle proposée, cette expression correspond          à une force centripète. affirmations 1 , 2 et 3 exactes,          l'affirmation 4 est fausse.                    

---

Pendule dans un          véhicule descendant une          côte                         
Déplacement sans frottement          et sans vitesse initiale.                        

L'angle q             est égal à l'angle a. 

Le pendule est à gauche             du support OA.

affirmations : 

-l'angle q             est nul
-la tension du fil a pour valeur             : T=mg cos a             / cosq.

                   

---

corrigé                   

---

      

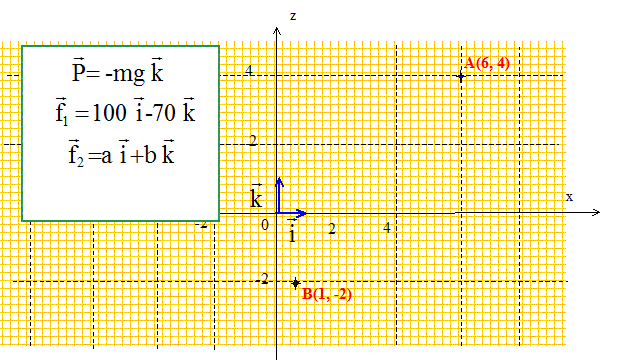
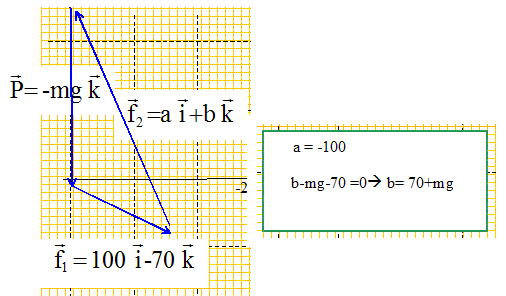
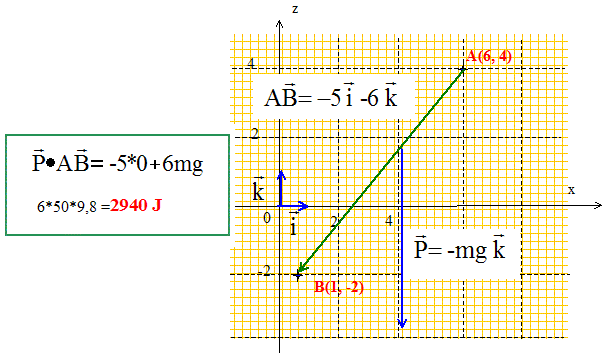
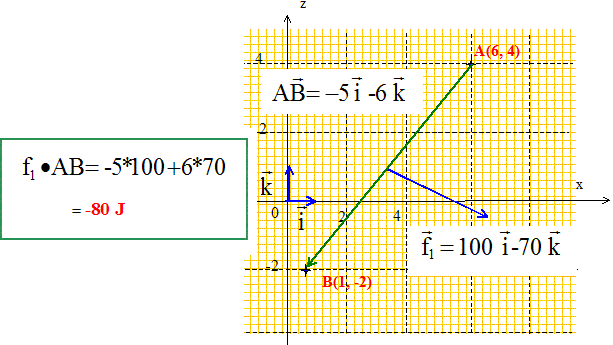
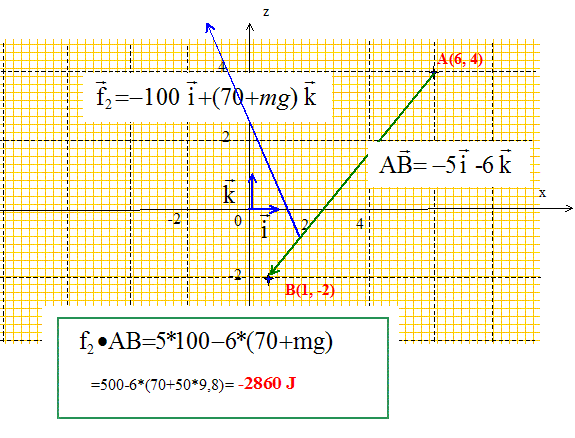
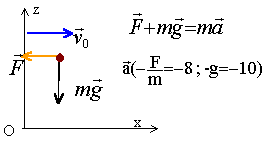
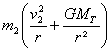
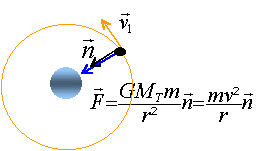
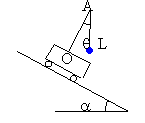
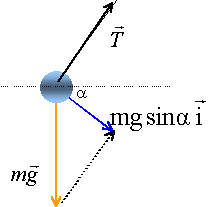                    l'accélération du véhicule est          égale à gsina.
La somme vectorielle des forces (poids et tension)          appliquée au pendule est donc colinéaire au          plan incliné. Cela entraîne q=0.
la tension du fil est mg cos a          . L'expression de la tension proposée est exacte car          cosq=cos0=1
affirmations 3 et 4 exactes,          affirmations 1 et 2 fausses.                   

---

Chute et rotation          de la terre                          
Vous êtes à Kuala          Lumpur quasiment situé sur l'équateur.

Un          jeune homme se penche par la fenêtre de la plus haute          tour du monde : orienté vers le nord, il lâche          une bille d'acier d'un point B. 

La fenêtre est          située à 405 m au dessus du sol. 

On rappelle          que la terre tourne de l'ouest vers l'Est et on admet          qu'elle effectue un tour en T=9 10⁴ secondes. On          néglige les frottements. 

affirmations :

-Le point d'impact de la bille             est à 4 km du pied de la tour vers l'ouest car la             terre a tourné. 

-Le point d'impact est au pied             de la tour (verticale de B).

-Le point d'impact est à             25 cm à l'ouest Le point d'impact est à             25 cm à l'est du pied de la tour (verticale de             B)                       

---

corrigé                   

---

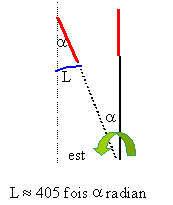                                En tenant compte du sens de la rotation de la terre, le          point d'impact est à l'est. Durée de la chute en négligeant les          frottements: 405=4,9 t² d'où t =9,1 s. angle décrit par la terre en 9,1 s : 2p          *9,1 / 9 10⁴ =6,35 10^-4 radian puis 405*6,35 10^-4 = 0,25 m. affirmation 4 exacte,          affirmations 1, 2 et 3 fausses. 

---

Le train          démarre.

Sur le quai d'une gare une          voyageuse en retard court pour essayer de prendre son train          à une vitesse constante v=8 m/s. Le train          démarre alors qu'elle est encore à une          distance d du dernier wagon. L'accélération          constante du train est 0,5 m/s². 

affirmations : 

-La voyageuse n'atteindra jamais le train si d est             supérieure à 64 m.

-Si d=60 m la voyageuse mettra 20 s pour atteindre le             dernier wagon.

-Si d=100 m la voyageuse s'approchera à 40 m du             dernier wagon.
-Si d=28 m la voyageuse mettra 4 s pour atteindre le             dernier wagon.


                   

---

corrigé                   

---

origine des distances le voyageur à t=0 ; le          dernier wagon du train est devant lui à la distance          d.                    distance parcourue par le voyageur (mouvement rectiligne          uniforme)
d₁=8t ; abscisse du voyageur x₁=8t          .
distance parcourue par le train
d₂=0,25 t² ; abscisse du dernier wagon :          x₂ = 0,25 t²+d
le voyageur rattrappe le train,          écrire x₁=x₂.
0,25 t²+d=8t ou 0,25 t²-8t+d=0
D=b²-4ac =64-d
si la distance est supérieure à 64 m, le          discriminant est nul, il n'y a pas de solution : le train          n'est pas rattrappé.
d=60 m : D= 4 et t = 12 s pour          atteindre le dernier wagon
d=28 m : D= 36 et t = 4 s pour          atteindre le dernier wagon                   

---

la distance est de 100m , x₂-x₁          est minimale lorsque sa dérivée est nulle          :
(0,25t²+100-8t)'=0,5t-8
d'où t=16s
le voyageur a parcouru : 8*16 = 128 m
le train se trouve à l'abscisse : 100+0,25          *16² = 164 m
distance entre le voyageur et le dernier wagon:          36 m.
affirmations 1 et 4 exactes,          affirmations 2 et 3 fausses.                   

---

Plan          incliné et contre poids.

Les forces de frottements          exercées sur le solide de masse m₁ sont          assimilées à une force colinéaire mais          de sens contraire à la vitesse. 

On communique une          vitesse initiale v₀ au solide de masse          m₁, parallèle au plan vers le          haut.

             
 

affirmations : 

-Si v₀=0 alors le             système reste en équilibre
  -Si v₀ non nulle et             pas de frottements alors le système a un mouvement             uniforme.v₀=0,5 m/s et pas de             frottement, la tension du fil vaut 5 N.
-v₀=0,5 m/s et             frottement =3N, la tension du fil vaut 8 N.


                   

---

corrigé                   

---

                                  vitessev v₀          nulle: s'il y a équilibre la somme vectorielle des forces          appliquées à la masse m₁ doit          être nulle. de plus T=m₂g =0,5*9,8 = 4,9 N m₁gsina =          1*9,8*sin30 = 4,9N si les frottements sont nuls, il y a          équilibre. si les frottements ne sont pas nuls, la somme vectorielle          des forces appliquées à m₁ n'est          pas nulle et il n'y a pas d'équilibre.                    

---

v₀ non nulle et          frottement nul :                    d'après le développement          précédent la somme vectorielle des forces          appliquées à m₁ est nulle. Le          principe d'inertie nous dit que le mouvement est rectiligne          uniforme.                    

---

v₀ =0,5 m/s et          frottement nul :                    mouvement rectiligne uniforme T=m₂g =4,9 N          voisin de 5 N.                    

---

v₀ =0,5 m/s et          frottementf=3N :                    somme vectorielle des forces appliquées à          m₁ = m₁ fois          accélération projection sur un axe parallèlle au plan vers le          haut : -m₁gsina +T-f =          m₁a -4,9-3 +T = a (1) lappliquons la seconde loi de Newton au solide          m₂: (axe vertical descendant) m₂g-T=m₂a 4,9 -T=0,5 a d'où a= 9,8 -2T repport dans (1). -7,9 +T = 9,8 -2T T= 5,9          N. affirmations 2 et 3 exactes,          affirmations 1 et 4 fausses. retour - menu

Electron et potentiel efom 2000

EFOM 2000
déviation des électrons

On négligera le poids des électrons devant les autres forces.
Une source S, dont le potentiel électrique V_S est nul, émet des électrons avec une vitesse pratiquement nulle. Ces électrons arrivent sur une grille G₁ au potentiel V₁.

-Exprimer la vitesse v₁ d'un électron passant par un trou de G₁, en fonction de la masse de l'électron m ,de V₁ et de la charge élémentaire e. Que se passerait-il si V₁ était négatif ?

-Au delà de G₁ à la distance d, est disposée une seconde grille G₂, parallèle à G₁, de potentiel V₂.
Déterminer les expressions en fonction du temps des coordonnées du vecteur vitesse d'un électron allant de O₁ à O₂.


-Un électron passe par un trou de G₂ à la vitesse v₂. Exprimer v₂ en fonction de e, m, et V₂. Déterminer sin i₂ en fonction de v₁, i₁, et v₂. Que se passerait-il si V₂ était négatif ?


-Etablir la relation entre i₁, i₂, V₁ et V₂.

---

corrigé

---

écrire le théorème de l'énergie cinétique entre la source et le point O₁.
la vitesse initiale est nulle. Le potentiel de la source S est nulle.
l'électron placé dans un champ électrique est soumis à une force électrique .
Le travail de cette force est : -e( V_S -V₁).
0,5 mv₁² -0 = eV₁.
v₁²=2eV₁/ m.
Si V₁ était négatif, le travail de la force électrique serait résistant et les électrons n'atteindraient jamais la grille G₁.

---

Entre G₁ et G₂ seule la force électrique intervient.
Seule la composante de la vitesse, dans la direction de la force, varie.
L'ordonnée du vecteur vitesse reste donc constante.
soit v₁ sin i₁ = v₂ sin i₂.(1)
 écrire le théorème de l'énergie cinétique entre G₁ et G₂.
la force électrique effectue le travail : -e(V₁-V₂)
si ( V₁-V₂) est négatif, les électrons sont déviés et accélérés entre les 2 grilles.
si ( V₁-V₂) est positif, les électrons sont déviés et freiné entre les 2 grilles : il se peut que la seconde grille ne soit pas atteinte.
0,5 mv₂² -0,5 mv₁² = -e(V₁-V₂)
avec 0,5 mv₁² = eV₁.
0,5 mv₂² -eV₁= -eV₁+eV₂.
v₂² =2eV₂ / m.
remplacer les vitesses par leurs expressions en fonction des potentiels électriques dans (1).

ressort efom 2000

E.F.O.M 2000

oscillateur mécanique

Deux ressorts R₁ et R₂ de constante de raideur K₁ et K₂ sont reliés entre eux par un crochet B, de masse négligeable. La masse m peut glisser sans frottement sur une tige horizontale.

1. On note x₁ et x₂ les élongations respectives à un instant t des 2 ressorts. Chaque élongation est comptée à partir de la position à vide du ressort correspondant. En appliquant le théorème du centre d'inertie au crochet B, établir la relation entre x₁ et x₂.
2. Exprimer x₁ en fonction de k₁, k₂ et de l'élongation totale x des 2 ressorts (avec x = x₁+x₂) .De même exprimer x₂ en fonction de k₁, k₂ et x.
3. Exprimer la somme des énergies potentielles élastiques des 2 ressorts en fonction de k₁, k₂ et x.
4. En utilisant la relation traduisant la conservation de l'énergie mécanique de ce système, établir l'équation différentielle de cet oscillateur (R₁, R₂ ,m). Exprimer sa pulsation propre w₀ en fonction de k₁, k₂ ,m.

---

corrigé

---

principe des actions mutuelles en B

x = x₁+x₂ et x₂ = k₁ x₁ / k₂d'où : x₁= x-k₁ x₁ / k₂
x₁ = k₂ x / (k₁+k₂) de même x₂ = k₁ x / (k₁+k₂)

---

énegie potentielle élastique d'un ressort : 0,5 k x². 0,5 k₁ x₁² + 0,5 k₂ x₂².
remplacer x₁ et x₂ par les expressions ci dessus.
mettre k₁k₂ / (k₁+k₂)² en facteur commun.
Ep =0,5 k₁k₂ / (k₁+k₂) x²

---

énergie mécanique = énergie cinétique + énergie potentielle. écrire la conservation de l'énergie mécanique du système constitué par les 2 ressorts et la masse m.
Em = 0,5 mv²+ 0,5 k₁k₂ / (k₁+k₂) x² = constante
dériver par rapport au temps ( u²)' = 2uu'
0,5 m *(2v'v) +0,5 k₁k₂ / (k₁+k₂) *(2xx') = 0
remarquer que x' =v et x"=v'
m x" x' + k₁k₂ / (k₁+k₂) x x' =0
diviser par x' chaque therme :
mx" + k₁k₂ / (k₁+k₂) x =0
cette expression liant la dérivée seconde x" et la fonction x est l'équation différentielle cherchée.

satellites, statique, cinématiques poitiers 1999

Terre et soleil
On donne c = 3 10⁸ m/s ; distance Terre-Soleil ~ 150 10⁶ km.  

Quelle proposition est vraie ?

- la vitesse du son dans l'air à 25°C est 340 km/s ( 340 m/s)
- la masse d'un électron est environ 10^-40 kg ( 10^-30 kg)
- le rayon de la Terre est de l'ordre de 4 10¹⁰ mm (4 10¹⁰ mm = 4 10⁷ m =4 10⁴ km : le rayon de la Terre est de l'ordre de 6400 km )
- il faut environ 8 min à la lumière émise par le soleil pour parvenir à la Terre
( 150 10⁹ / 3 10⁸ = 500 s ~8,3 min) Vrai.
- l'accélération de la pesanteur sur la Lune est 60 fois plus faible que sur la Terre ( 6 fois plus faible que sur Terre).

---

POINT mobile

Les coordonnées du vecteur position et du vecteur vitesse d'un mobile ponctuel 
aux dates t₁ = 2s, t₂ =4 s et t₃ = 5 s sont les suivantes :

date t(s)	position (m)	vitesse (m s-1)
2	x=4	x'=4
	y=8	y'=8
	z=0	z'=0
4	x=16	x'=8
	y=32	y'=16
	z=0	z'=0
5	x=25	x'=10
	y=50	y'=20
	z=0	z'=0

A la date t=0, x₀=y₀=z₀=0. 




Ces données sont compatibles avec certaines des hypothèses suivantes,  
précisez lesquelles :
- le mouvement est plan ( z = 0 et z' =0 aux trois dates ) Vrai
- le mouvement est rectiligne ( quand x est multiplié par 4, y est multiplié par 4 ; quand x est multiplié par 5, y est multiplié par 5 ) Vrai
- le mouvement est uniforme ( uniforme signifie : la norme de la vitesse est constante )
- les coordonnées de l'accélération sont a_x=2 m s^-2 ; a_y =2 m s^-2 ; a_z = 0.
(Dx'/Dt = (8-4) / 2 = 2 ou (10-4) / 3 = 2 ; Dy'/Dt = (16-8) / 2 = 4 ou (20-8) / 3 = 4 )
- à la date t=0 les composantes de la vitesses sont nulles.Vrai
x'(2) = a_x t+ x'₀ ; 4 = 2*2 +x'₀ d'où x'₀ =0
y'(2) = a_y t+ y'₀ ; 8 = 4*2 +y'₀ d'oùy'₀ =0

 



Un mobile ponctuel M se déplace dans un plan muni d'un repère d'espace orthonormé ( O, i, j) (Les vecteurs sont écrits en gras et en bleu)
A chaque instant t OM = (t+2) i + (3t²+5t) j.
Ces données sont compatibles avec certaines des hypothèses suivantes,  
précisez lesquelles :
- le mobile a un mouvement rectiligne et uniformément varié
x = t+ 2 soit t = x-2 ; y = 3t²+5t = 3( x-2)² + 5(x-2)
y = 3x²-12x +12+5x-10 ; y = 3x²-7x +2 ( parabole)
- le mobile a une trajectoire parabolique ( Vrai)
- le vecteur vitesse du mobile est constant ( v =dOM /dt = 2 i + (6t+5) j )
- le vecteur accélération du mobile est constant ( a =dv /dt = 0 i + 6 j ) ( Vrai)
- à l'instant t=0, initial, le vecteur vitesse est : v₀ = i.
( v =dOM /dt = 2 i + (6t+5) j ; v₀ = 2 i +5 j )

---

 Décomposition de forces :

On décompose une force F en deux composantes F₁ et F₂ .

a =30 ° ; ß = 45° ; norme de F = 10 N.

Dans ces conditions, les intensités F₁ et F₂ des forces sont :

F₁ = F₂ = 5 N ;
F₁ =8,3 N, F₂ = 6,2 N ;  
F₁ =7,3 N, F₂ = 5,2 N ;
F₁ =7,3 N, F₂ = 8,3 N ;
F₁ =8,3 N, F₂ = 5,2 N.

---

 Terre et satellite

Dans le référentiel géocentrique supposé galiléen, un satellite de la terre décrit une orbite circulaire de rayon R.
- la norme de sa vitesse est constante ( Vrai )
- son accélération est nulle ( a_N = v²/R)
- sa période de révolution est proportionnelle au rayon ( 3^è loi de Kepler T² = constante fois R³ )
- si le satellite est géostationnaire, sa vitesse est nulle
- on pourrait placer un satellite de vitesse différente sur la même orbite.



La période de rotation de la Terre dans un référentiel géocentrique vaut 86164 s. 
La Terre est supposée sphérique et de rayon R = 6370 km.

L'accélération d'un point de la Terre de latitude 45° vaut :

2,39 10^-2 m s^-2 ; 
3,38 10^-2 m s^-2 ; 
1,69 10^-2 m s^-2 ; 
2,39 cm s^-2 ; 
3,38 cm s^-2 ;

---

L'intensité de la force gravitationnelle exercée par la Terre sur la Lune vaut 1,98 10²⁶ N. 
La masse de la Terre vaut environ 80 fois la masse de la Lune.
Le rayon terrestre est 3,66 fois celui de la Lune.

L'intensité de la force gravitationnelle exercée par la Lune sur la Terre vaut donc :

1,84 10²³ N ; 2,48 10²⁴ N ; 1,48 10²⁵ N ; 5,41 10²⁵ N ; 1,98 10²⁶ N.
La force attractive exercé par la Terre sur la Lune a même valeur que la force attractive exercée par la Lune sur la Terre.

---

gravitation et satellite

Au cours de son exploration du système solaire, une sonde Voyager, de masse M = 2l00 kg, s'est approchée d'une planète notée A. On a mesuré à deux altitudes différentes comptées à partir du sol de cette planète la force de gravitation exercée par celle-ci sur la sonde soit:
z₁ = 8 499 km donne F₁ =13 236,51 N
altitude z₂ = 250 000 km donne F2 =189,25 N

Données : masse de la Terre: M_T = 5,98. 10²⁴ kg ; C^te de gravitation K= 6,67. 10^-11
Masses des planètes du système solaire: (la masse de la Terre étant prise égale à l'unité)
Terre 1
Mercure 0,056
Vénus 0,817
Mars 0,11 Jupiter 318 Saturne 95,2 Uranus 14,6 Neptune 17 Lune 0,012

Parmi les unités écrites ci-dessous, laquelle convient pour exprimer le champ de gravitation?
N / m ; m . s² ; m / s ; N / kg ; kg / N ; kg / m² ; kg / m² ; m² / s² ; kg /m

Calculer le diamètre moyen de la planète A.(unité: 10³ km)
50,5 ; 48,6 ; 12,1 ; 6,77 ; 138 ; 11,4 ; 4,88 ; 3,48

Quelle est l'intensité du champ de gravitation au niveau du sol de la planète A? (unité S.I)
1,66 ; 3,78 ; 8,62 ; 22,93 ; 11,48 ; 9,05 ; 7,84 ; 2,57

Quel est le nom de la planète A?
mercure ; vénus ; lune ; jupiter ; saturne ; mars ; uranus ; neptune

La planète A possède un satellite de rayon R =1350 km dont la période de révolution autour de A (sur une trajectoire supposée circulaire) vaut T_S = 5 j 2l h 03 min.
calculer la distance séparant le centre du satellite au centre de la planète A (unité 10³ km)
18,8 ; 188 ; 353,8 ; 419,7 ; 253,8 ; 92,6 ; 543,6 ; 612,5 

---

corrigé
Il suffit de penser à : P = mg poids(N) = masse (kg) fois accélération de la pesanteur (m/s² ou N/kg)

---

champs et forces sont proportionels. La c^te de proportionalité est la masse du satellite. champ à une altitude h d'où F₁ * (R+h₁)² = F₂ * (R+h₂)² (forces en N et distance en m)
R= 24,26 10³ km D=48,52 10³ km

---

champ au sol: g₀= g (R+h)²/R² et g= Force/M_satellite g₀= 11,5 ms^-2.

---

masse planète en kg et rayon planète en m.
d'où masse planète = 1,015 10²⁶ kg
rapport des masses de cette planète à celle de la terre :(diviser par la masse de la terre le résultat précédent) : 17
lire dans le tableau ci dessus : neptune.

---

3^ème loi de képler :

période en seconde, distance en mètre, masse en kg.
R+h = 353,7 10³ km.

Ondes

Ondes.

(manip radio Montpellier 2008)

Soit une sonde située à une distance d=5,4 m d'une paroi réfléchissante.
La sonde joue à la fois le rôle d'émetteur et de récepteur : elle émet des salves d'ultrasons ;
ces ondes se réfléchissent sur la paroi et sont détectées par la sonde.
La célérité c de ces ondes ultrasonores est de 360 m/s dans les conditions de l'expérience.

Déterminer, en ms, l'intervalle de temps Dt séparant l'émission d'une salve d'ultrasons et sa réception par la sonde.

Dt = 2d/c ; Dt = 2*5,4 / 360 = 5,4 / 180 = 3*1,8 / (1,8*100) = 0,03 s = 30 ms.


--------------------------------------------------------------------------------
Un haut parleur émet une onde sonore progressive sinusoïdale de fréquence f= 1,2 kHz.
Deux microphones sont placés dans l'axe du haut parleur, en un point A et en un point B, avec AB = 45 cm. L'onde sonore se propage dans l'air à la clérité c = 360 m/s.

Comment vibrent les ondes en A et en B ? Justifier.

Calcul de la longueur d'onde l : l = c/f = 360 / 1200 =3,6 / 12 =36 10-1/12 = 0,3 m = 30 cm.

La distance AB est égal à 3*15 cm soit un nombre impair de demi-longueur d'onde.

En conséquence les points A et B vibrent en opposition de phase.


Soit une onde lumineuse se propageant dans le vide. Sa longueur d'onde est l0=750 nm.

Quelle est sa couleur ? Rouge.

Cette onde se propage maintenant dans un milieu transparent d'indice n=1,5.

Déterminer sa longueur d'onde l en nm dans ce milieu.

indice de réfraction n = célérité de l'onde dans le vide / célérité de l'onde dans le milieu ; n = c/cM.

La fréquence f d'une onde caractérise une onde ; elle ne dépend pas du milieu de propagation.

Or c =l0 f et cM =l f d'où n =l0/l.

l =l0/n = 750/1,5 = 500 nm.

Quelle est sa couleur ? Justifier.

L'oeil est sensible à l'énergie qu'il reçoit ; l'énergie est proportionnelle à la fréquence de la radiation : celle-ci étant constante, la couleur de la radiation est rouge

---