On considère un ressort R de constante de raideur k inconnue. Lorsqu'on suspend à son extremité libre une masse m1 =25 g, sa longueur est L1=18,5cm ; lorsqu'on suspend une masse m2=45 g sa longueur est L2=20,5cm.
Déterminer la valeur de la raideur k et celle de la longueur à vide L0 du ressort.
L'extrémité inférieure du ressort est soumise à :
l'action de la masse, verticale vers le bas, valeur P=mg ( masse en kg)
à la tension du ressort, verticale vers le haut, valeur T= k x ( k : raideur en N/kg et x : allongement en m)
T= mg = kx
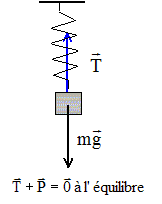
m1g = k(L1-L0) = kL1-kL0 (1)
m2g = k(L2-L0) = kL2-kL0 (2)
(2)-(1) donne : k(L2-L1) = (m2-m1)g
L2-L1 = 0,02 m ; m2-m1 = 0,02 kg
k = 0,02*9,8/0,02 = 9,8 N/m.
L0 = L1-m1g/k = 0,185-0,025*9,8 /9,8 = 0,16 m = 16 cm.
Déterminer le travail du poids lors de l'allongement du ressort dans le cas où m2=45 g :
Le travail d'une force constante ne dépend que des positions finale et initiale.
En descente le travail du poids est moteur et vaut :
W=m2g ( L2-L0)
W= 0,045*9,8 *0,045 =0,02 J.
Un solide de m =50 kg est en mouvement dans le repère orthonormé (O, i, k).
Il est animé d'un mouvement rectiligne uniforme et il est soumis aux forces P, f1, f2 telle que :
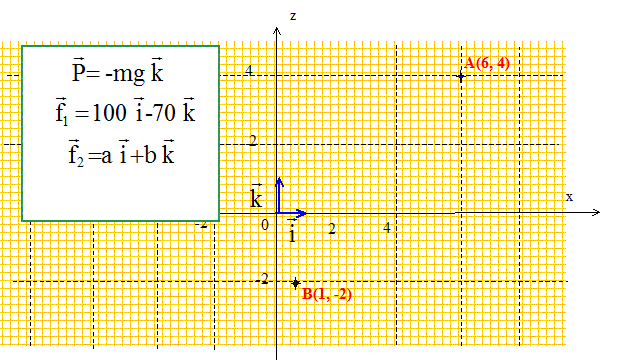
Exprimer la force f2 en fonction des vecteurs i et k.
Correction : D'après le principe d'inertie, la somme vectorielle des forces est nulle.
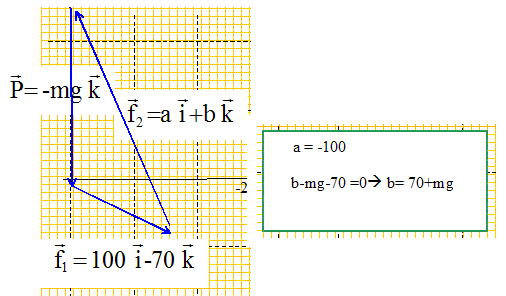 |
Calculer les travaux des forces exercées sur le solide entre A et B :
Correction : Travail du poids :
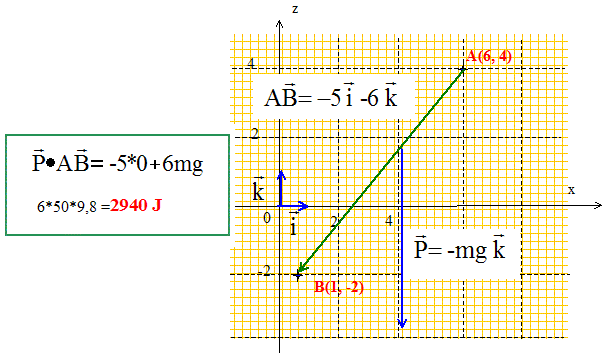
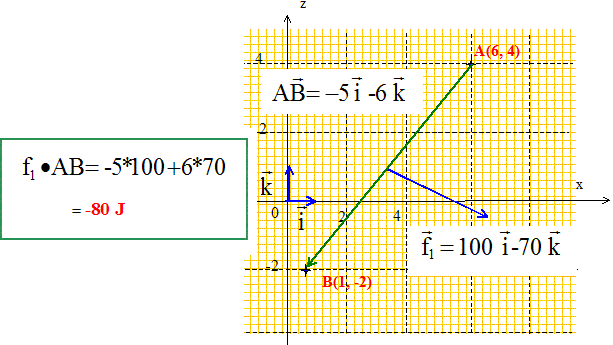
Travail de f2 :
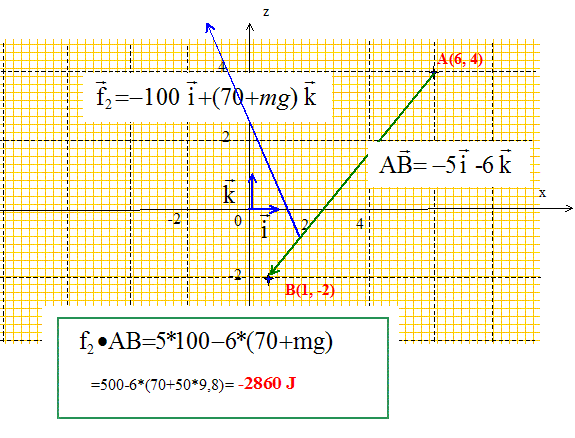
Remarque : la somme des travaux est nulle.