Régimes transitoires électriques concours kiné Nantes 2009.

Rappel : si x est une grandeur fonction du temps satisfaisant à l'équation différentielle τdx(t)/dt + x(t) = H
où t et H sont constants,
x(t) est de la forme générale : x(t) = K exp^(-t/τ) + H.
K est une constante que l'on détermine en considérant les conditions initiales.


On réalise le montage ci dessous :

Le générateur est une source idéale de tension de fem E = 6,0 V.

A t = 0 on relie les points O et A.

Question : Représenter le circuit parcouru par le courant i(t), et noter les tensions u_L(t) aux bornes de l'inductance L et u_r(t) aux bornes de la résistance r.

Question : Etablir l'équation différentielle relative à i(t).

Additivité des tensions : u_L(t) + u_r(t) = E.

Ldi(t)/dt + r i(t) = E.
L/r di(t)/dt + i(t) = E / r.
Question : Préciser les valeurs de l'intensité i(t) aux dates t=0 et t très grand ( régime permanent ).

A la date t₀^-, la bobine ne stocke pas d'énergie : i(t₀^-) =0.

La continuité de l'intensité conduit à : i(t₀⁺) =0 : donc i(t=0) = 0.
En régime permanent, l'intensité est constante et di(t)/dt = 0, d'où i(t_oo) = E/r.

Question : Déterminer la constante de temps t₁ en fonction de L et r et donner l'expression littérale de i(t).

t₁ = L/r ; i(t) = K exp(-t/t₁) + E/r ; i(0) = 0 = K + E/r soit K = -E/r.

i(t) = E/r ( 1-exp(-t/t₁)


Question : On coupe la connexion entre O et A.

Le condensateur étant déchargé, on relie O à B à un instant choisit comme nouvelle origine des temps. Représenter le circuit parcouru par le courant i₂(t) ; noter la charge q(t) du condensateur de capacité C, la tension u_C(t) aux bornes du condensateur et la tension u_R(t) aux bornes du conducteur ohmique de résistance R

Question : Etablir l'équation différentielle relative à q(t). Additivité des tensions : u_C(t) + u_R(t) = E.
q(t) / C + R i₂(t) = E avec i₂(t) = dq(t) / dt :
q(t) / C + R dq(t) / dt = E
RC dq(t)/dt + q(t) = CE.

Question : Préciser les valeurs de la charge q(t) aux dates t=0 et t très grand ( régime permanent ).

A la date t₀^-, le condensateur ne stocke pas d'énergie : q(t₀^-) =0.

La continuité de la charge conduit à : q(t₀⁺) =0 : donc q(t=0) = 0.
En régime permanent, la charge est constante et dq(t)/dt = 0, d'où q(t_oo) = CE

Question : Déterminer la constante de temps t₂ en fonction de C et R et donner l'expression littérale de q(t).
t₂ = RC ; q(t) = K exp(-t/t₂) + EC ; q(0) = 0 = K + EC soit K = -EC.
q(t) = EC ( 1-exp(-t/t₂).

Question : Donner l'expression littérale de i₂(t).
i₂(t) = dq(t)/dt = EC / t₂ exp(-t/t₂) ; i₂(t)= E/R exp(-t/t₂).

Question : Le condensateur étant de nouveau déchargé, on relie à l'instant t=0, le point O à la fois à A et B. L'intensité débitée par le générateur de fem E est notée i₃.
Rappeler la loi des noeuds reliant à chaque instant i(t), i₂(t) et i₃(t).

Au noeud O : i₃(t) = i(t) + i₂(t).

Question : Les expressions de i(t), i₂(t) étant celles obtenues ci-dessus, donner l'expression littérale de i₃(t).

i₃(t) = E/R exp(-t/t₂) + E/r ( 1-exp(-t/t₁)).
i₃(t) = E [ 1/R exp(-t/t₂) - 1/r exp(-t/t₁) + 1/r]

Question : Exprimer les conditions que doivent vérifier les valeurs associées aux composants pour que i₃(t) soit indépendant de t.

1/R exp(-t/t₂) - 1/r exp(-t/t₁) doit être nulle.
d'où : R = r et t₁= t₂ ; L/r = RC ; L = rRC ; L= R²C.
A.N : C = 1,0 µF et R = 1,0 kW.
par suite : r = 1,0 kW ; L = 10⁶*10^-6 = 1,0 F.

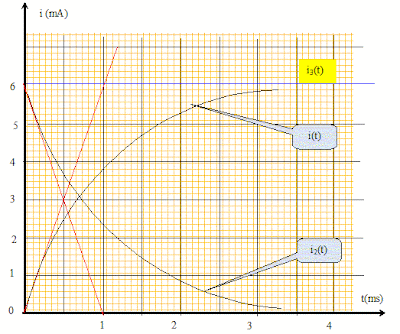
Question : Tracer sur le même graphique i(t), i₂(t) et i₃(t) avec les tangentes à l'origine.
t₁= t₂ = 10^-3 s = 1 ms ; i(t) = 6/1000 ( 1-exp(-t))= 6(1-exp(-t)) avec i en mA et t en ms.
i₂(t) = 6 exp(-t) avec i₂ en mA et t en ms.
i₃(t) =6 exp(-t) + 6 ( 1-exp(-t) ; i₃(t)=6 mA

Question : Les valeurs des composants étant celles calculées précédemment, on réalise une nouvelle expérience.
Après avoir chargé le condensateur au maximum ( charge q = Q₀), on relie à l'instant t = 0, le point B au point A ( C, L, R et r sont en série).  
Représenter le circuit parcouru par le courant i₁(t) ; noter la charge q(t) du condensateur de capacité C

Question : Montrer que la constante de temps s'exprime par t₁ = (LC)^½. On notera par la suite t = (LC)^½.
t₁ =L/r = L/R et L = R²C ; R = L^½ C^-½ ; par suite : t₁ = L^½C^½.
Question : Ecrire l'équation différentielle relative à q(t) où l'on fera apparaître t

Question : Le régime est alors dit apériodique critique. q(t) est de la forme q(t) = (a+ßt) exp(-t/t) où a et ß sont des constantes.
Préciser les valeurs de la charge q et de l'intensité i₁ à t=0 ; en déduire l'expression de q(t).

Le condensateur est chargé au maximum à t = 0 : q(0) = Q₀ = CE = 6 10^-6 C = 6 µC.
La bobine ne stocke pas d'énergie à t = 0 : i(0) = 0.
q(0) = a exp(0) = a = CE = 6 µC.
i₁(t) = dq/dt = ß exp(-t/t) + (a+ßt) (-1/t ) exp(-t/t)
i₁(0) = 0 = ß- a/t = 0 ; ß = a/t = CE ( LC)^-½ = 6 10^-6 (1*10^-6)^-½ ; ß = 6 10^-3 C s^-1.
( LC)^½ = (1*10^-6)^½ = 10^-3 s = 1 ms.
q(t) = 6 (10^-6+10^-3 t ) exp(-1000t) = 6 10^-6 (1 +1000t)exp(-1000t)
q(t) = 6(1+t) exp(-t) avec q en µC et t en ms